https://en.wikipedia.org/wiki/Inclusion%E2%80%93exclusion_principle
the inclusion–exclusion principle is a counting technique which generalizes the familiar method of obtaining the number of elements in the union of two finite sets; symbolically expressed as
The principle is more clearly seen in the case of three sets, which for the sets A, B and C is given by
Suppose we want to determine the number of derangements of the n integers 1,2,...,n for n bigger than 2. Let us focus on k and move it into the first position. We thus have started a derangement, for 1 is not in its natural position. Where could 1 be placed? There are two cases we could consider: either 1 is in position k or 1 is not in position k.
If 1 is in position k, here's what we know: The integers 1 and k have simply traded positions.
Indicated by the question marks, there are (n-2) integers yet to derange. This can be done in D(n-2) ways.
If 1 is not in position k, we don't know as much. Note that we have shown 1 as a prohibited value twice. This is required for this case, because we cannot have 1 appear in the first position (its natural position) nor can 1 appear in position k.
Indicated by the question marks, there are now (n-1) integers yet to derange. This can be done in D(n-1) ways.
Putting this together, we have D(n-1) + D(n-2) possible derangements when k is in the first position. How many different integers could we put in position 1 and carry out this process? All the integers except 1. that is, (n-1) different integers.
This yields the recursive formula D(n) = (n-1)[D(n-1) + D(n-2)]. As long as we know D(1) = 0 and D(2) = 1, we can generate subsequent values for D(n).
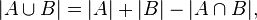

No comments:
Post a Comment