https://en.wikipedia.org/wiki/Coupon_collector%27s_problem
the coupon collector's problem describes the "collect all coupons and win" contests. It asks the following question: Suppose that there is an urn of n different coupons, from which coupons are being collected, equally likely, with replacement. What is the probability that more than tsample trials are needed to collect all n coupons? An alternative statement is: Given n coupons, how many coupons do you expect you need to draw with replacement before having drawn each coupon at least once? The mathematical analysis of the problem reveals that the expected number of trials needed grows as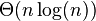 .[1] For example, when n = 50 it takes about 225[2] trials to collect all 50 coupons.
.[1] For example, when n = 50 it takes about 225[2] trials to collect all 50 coupons.
赠券收集问题
the coupon collector's problem describes the "collect all coupons and win" contests. It asks the following question: Suppose that there is an urn of n different coupons, from which coupons are being collected, equally likely, with replacement. What is the probability that more than tsample trials are needed to collect all n coupons? An alternative statement is: Given n coupons, how many coupons do you expect you need to draw with replacement before having drawn each coupon at least once? The mathematical analysis of the problem reveals that the expected number of trials needed grows as
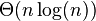 .[1] For example, when n = 50 it takes about 225[2] trials to collect all 50 coupons.
.[1] For example, when n = 50 it takes about 225[2] trials to collect all 50 coupons.赠券收集问题
赠券收集问题的特征是开始收集时,可以在短时间内收集多种不同的赠券,但最后数种则要花很长时间才能集齐。例如有50种赠券,在集齐49种以后要约多50次收集才能找到最后一张,所以赠券收集问题的答案t的期望值要比50要大得多。
以一个例子来说明:有种食品每袋都会附赠一张卡片,共有10种卡片,每种卡片出现的概率相等。
首先来求当拥有i种卡片时,再拆开一袋得到不同卡片的概率Pi:
a. 当我们没有任何卡片时,随意拆开就能得到一种不同的卡片,即第一种得到的卡片P0 = 1
b. 当有了一种继续拆,此时得到新的种类的概率为P1 = 9 / 10
...当有了i种,此时得到新种类的概率为Pi = (10 - i) / 10
...当有了i种,此时得到新种类的概率为Pi = (10 - i) / 10
我们知道了Pi的值,那么对于拆了i包后,拆开发现新卡片的次数期望为E = Pi * Ni,由于只需要然其发生一次即可令E=1反过来求对应的Ni,Ni = 1 / Pi,即拆1 / Pi包时可以发现一种新卡片(相对于已经拥有i种卡片)。
那么发现全部卡片总共需要的包数 = N0 + N1 + N2 ... N9 = 10 / 10 + 10 / 9 + 10 / 8 ... 10 / 1 = 29.289682539682538
即按期望来,买30包可以集齐卡片。
下面给出了卡片等概率出现时,集齐卡片的期望次数:
1 1.0
2 3.0
3 5.5
4 8.33333333333
5 11.4166666667
6 14.7
7 18.15
8 21.7428571429
9 25.4607142857
10 29.2896825397
11 33.2186507937
12 37.2385281385
13 41.3417388167
14 45.5218725719
15 49.7734348984
16 54.0916638917
17 58.4723928849
18 62.9119454075
19 67.4070534857
20 71.9547931429
21 76.5525328
22 81.1978915048
23 85.888704755
24 90.6229962661
25 95.3989544438
26 100.214912622
27 105.069332338
28 109.960789091
29 114.88796013
30 119.849613928
31 124.844601059
32 129.871846254
33 134.930341449
34 140.019139675
35 145.137349666
36 150.284131085
37 155.458690281
38 160.660276505
39 165.888178519
40 171.141721557
41 176.420264596
42 181.723197879
43 187.049940686
44 192.399939306
45 197.7726652
46 203.167613315
47 208.584300561
48 214.022264403
49 219.481061578
50 224.960266916
51 230.459472255
52 235.978285436
53 241.516329387
54 247.073241262
55 252.648671656
56 258.242283868
57 263.853753223
58 269.482766437
59 275.129021031
60 280.792224777
61 286.47209519
62 292.168359046
63 297.880751933
64 303.609017837
65 309.352908741
66 315.11218426
67 320.886611294
68 326.675963702
69 332.480021991
70 338.298573035
71 344.131409792
72 349.978331057
73 355.839141211
74 361.713649994
75 367.601672291
76 373.503027922
77 379.417541447
78 385.345041986
79 391.285363037
80 397.238342316
81 403.203821595
82 409.181646553
83 415.171666632
84 421.173734905
85 427.18770794
86 433.21344568
87 439.250811328
88 445.299671228
89 451.359894765
90 457.431354256
91 463.513924859
92 469.607484473
93 475.711913652
94 481.827095519
95 487.952915684
96 494.089262165
97 500.236025313
98 506.393097739
99 512.560374246
100 518.737751764
101 524.925129282
102 531.122407789
103 537.329490219
104 543.546281386
105 549.772687938
106 556.008618299
107 562.253982622
108 568.50869274
109 574.772662118
110 581.045805807
111 587.328040405
112 593.619284012
113 599.919456191
114 606.228477927
115 612.546271593
116 618.872760911
117 625.207870919
118 631.551527936
119 637.903659528
E = n / n + n / (n-1) + n/ (n-2) ... n / 1
当卡片出现的概率不是相等的时候,Pi的计算过程就麻烦许多
No comments:
Post a Comment