Modular multiplicative inverse - Wikipedia, the free encyclopedia

In modular arithmetic, the modular multiplicative inverse of an integer a modulo m is an integer x such that

That is, it is the multiplicative inverse in the ring of integers modulo m, denoted .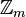

Once defined, x may be noted , where the fact that the inversion is m-modular is implicit.

The multiplicative inverse of a modulo m exists if and only if a and m are coprime (i.e., if gcd(a, m) = 1). If the modular multiplicative inverse of a modulo m exists, the operation of division by a modulo m can be defined as multiplying by the inverse, which is in essence the same concept as division in the field of reals.

Read full article from Modular multiplicative inverse - Wikipedia, the free encyclopedia