Documents and queries are represented as vectors by .
Each dimension corresponds to a separate term. If a term occurs in the document, its value in the vector is non-zero. Several different ways of computing these values, also known as (term) weights, have been developed. One of the best known schemes is tf-idf weighting (see the example below).
The definition of term depends on the application. Typically terms are single words, keywords, or longer phrases. If the words are chosen to be the terms, the dimensionality of the vector is the number of words in the vocabulary (the number of distinct words occurring in the corpus).
Vector operations can be used to compare documents with queries.
Applications[edit]
Relevance rankings of documents in a keyword search can be calculated, using the assumptions of document similarities theory, by comparing the deviation of angles between each document vector and the original query vector where the query is represented as the same kind of vector as the documents.
In practice, it is easier to calculate the cosine of the angle between the vectors, instead of the angle itself:
Where 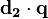 is the intersection (i.e. the dot product) of the document (d2 in the figure to the right) and the query (q in the figure) vectors,
is the intersection (i.e. the dot product) of the document (d2 in the figure to the right) and the query (q in the figure) vectors,  is the norm of vector d2, and
is the norm of vector d2, and 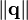 is the norm of vector q. The norm of a vector is calculated as such:
is the norm of vector q. The norm of a vector is calculated as such:
As all vectors under consideration by this model are elementwise nonnegative, a cosine value of zero means that the query and document vector are orthogonal and have no match (i.e. the query term does not exist in the document being considered). See cosine similarity for further information.
Example: tf-idf weights[edit]
In the classic vector space model proposed by Salton, Wong and Yang [1] the term-specific weights in the document vectors are products of local and global parameters. The model is known as term frequency-inverse document frequency model. The weight vector for document d is ![\mathbf{v}_d = [w_{1,d}, w_{2,d}, \ldots, w_{N,d}]^T](http://upload.wikimedia.org/math/3/c/9/3c90fef2940856f7410b65d07e31fd4f.png) , where
, where
and
 is term frequency of term t in document d (a local parameter)
is term frequency of term t in document d (a local parameter) is inverse document frequency (a global parameter).
is inverse document frequency (a global parameter).  is the total number of documents in the document set;
is the total number of documents in the document set; 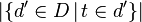 is the number of documents containing the term t.
is the number of documents containing the term t.
Using the cosine the similarity between document dj and query q can be calculated as:
Read full article from Vector space model - Wikipedia, the free encyclopedia




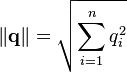
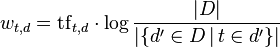
 is term frequency of term t in document d (a local parameter)
is term frequency of term t in document d (a local parameter) is inverse document frequency (a global parameter).
is inverse document frequency (a global parameter).  is the total number of documents in the document set;
is the total number of documents in the document set; 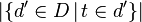 is the number of documents containing the term t.
is the number of documents containing the term t.