We saw in the previous section on dot products that the dot product takes two vectors and produces a scalar, making it an example of a scalar product. In this section, we will introduce a vector product, a multiplication rule that takes two vectors and produces a new vector. We will find that this new operation, the cross product, is only valid for our 3-dimensional vectors, and cannot be defined in the 2- dimensional case.
One important feature of the dot product is its invariance under rotations.In other words, if we take a pair of vectors in the plane and rotate them both by the same angle, their dot product will remain the same. Consider the length of a single vector (which is given by the dot product): if the vector gets rotated about the origin by some angle, its length will not change--even though its direction can change quite dramatically! Similarly, from the geometric formula for the dot product, we see that the result depends only on the lengths of the two vectors and the angle between them. None of these quantities changes when we rotate the two vectors together, so neither can their dot product. This is what we mean when we say that the dot product is invariant under rotations.
Let's begin by defining the cross product for the unit vectors i , j , and k . Since all vectors can be decomposed in terms of unit vectors (see Unit vectors), once we've defined the cross products for this special case it will be easy to extend the definition to include all vectors. As we noted above, the cross product between iand j (since they both lie in the x - y plane) must point purely in the z -direction. Hence:
i×j = c k
for some constant c . Because later on we will want the magnitude of the resultant vector to have geometric significance, we need c k to have unit length. In other words, c can be either +1 or -1. Now we make a completely arbitrary choice in order to accord with convention: we choose c = + 1 . The fact that we have chosen c to be positive is known as The Right-Hand Rule.
| i×j | = | k = - j×i | |
| j×k | = | i = - k×j | |
| k×i | = | j = - i×k |
| i×i = j×j = k×k = 0 |
| u×v = ab(i×j) = ab k |
| | u×v| = | u|| v| sinθ |
Cross Product Summary
| u×v = (u 1 v 2 - u 2 v 1)k + (u 3 v 1 - u 1 v 3)j + (u 2 v 3 - u 3 v 2)i |

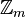 .
. , where the fact that the inversion is m-modular is implicit.
, where the fact that the inversion is m-modular is implicit.

